Computational physics Lecture: 1 introduction
Computational
physics
Lecture: 1 introduction
Purpose of
Course
The purpose of this course is demonstrate to students how computers
can enable us to both broaden and deepen our understanding of physics by vastly
increasing the range of mathematical calculations which we can conveniently perform.
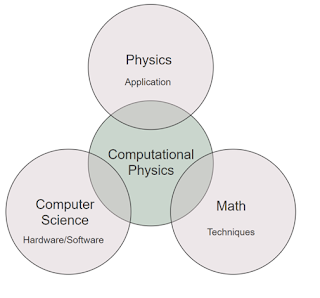
Computational physics diagram
Suppose you take an introductory
calculus-based physics course; you will have learned all about Newton’s laws of
motion and solved many problems with an analytical approach. However, one
problem you will not have solved is a simple problem of throwing a ball while
including air resistance. One of the reasons you didn’t solve this problem is
that it’s impossible to solve analytically, since air resistance is a nonlinear
force 1. However, adding air resistance which is proportional to the
square of the particle’s velocity, while impossible to solve analytically, is
not so complicated to solve computationally. So, one of the great uses of computation is
to be able to solve problems via computer that are difficult or impossible to
solve with pen and paper. Such problems can range from solving non-linear
differential equations, to systems which involve random processes (for instance, diffusion, or disease propagation), and
even the everyday work of processing and visualizing data.
1 Actually, it’s even worse—air resistance is
not really a simple function of velocity at all; for low velocities, one can
approximate the air resistance as linear, and but as the speed increases, it’s
not even correct to treat it as a simple function of the velocity to a fixed
power
On the other hand, physics has been
divided into two categories: theoretical and experimental physics. However,
over the past few years computational physics has emerged as a third discipline
which can perhaps be placed between these two. This field of investigation consists
of the study of physical systems with the help of computer power.
The reasons for the increasing relevance of
computational physics are manifold. In theoretical physics, many problems exist
that cannot be solved analytically with pencil and paper. One can turn to
analytical approximation methods but these have often limits regarding their
applicability or accuracy. When the underlying physical system is very complex,
many times analytical methods are either too time consuming or simply
unattainable. Moreover, one might be dealing with stochastic processes where
conclusions about the system can only be drawn from simulating it many times
over. This is where computers can make a big difference in allowing for the
computation of system dynamics or characteristics.
In experimental physics, computers can help in
interpreting complex data sets, guide experiments and experimental set ups, and
even facilitate virtual experiments by use of modelling and simulation. The
latter can replace expensive experiments, for example, or provide insights into
the dynamics in certain locations within a physical system which are not
accessible by measurement techniques.
Since computers represent numbers by a finite set of
zeros and ones, the precision of calculations has its own limits. Therefore,
studying and assessing errors that computational predictions inherently contain
is a major field in its own right.
The bottom line is that every student is well advised
to familiarize themselves with computational physics. Throughout the career of
a future scientist, there will be no escaping from the use of it.
Software
There are many types of computer software programs
used in computational physics, such as:
Homework (give some examples)
Examples of daily life problems that solved
by computational physics:
·
Weather
models, expecting future weather.
·
Homework (give some examples)
Introduction to functions
A function is a
rule which operates on one number to give another number. However, not every rule
describes a valid function. This unit explains how to see whether a given rule describes
a valid function, and introduces some of the mathematical terms associated with
functions. Read
more
Homework (State at least three functions and its physical meaning)
تعليقات
إرسال تعليق